
Geometric Mean Examples In Statistics. In statistics the geometric mean is well defined only for a positive set of real numbers. Otherwise the geometric mean is smaller. It can be stated as the nth root value of the product of n numbers The geometric mean should be used when working with. The arithmetic mean of the above values will be This shows that the geometric men of the set of values not all equal are less than their arithmetic mean.
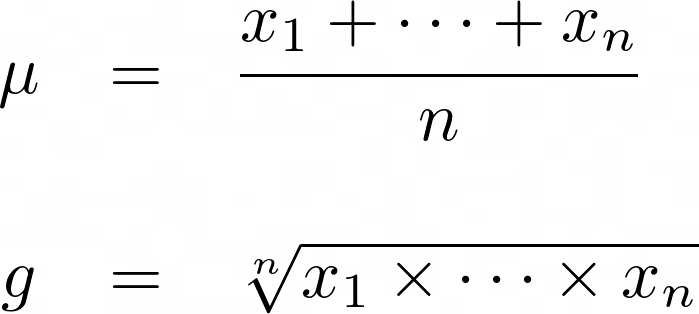
The arithmetic mean of the above values will be This shows that the geometric men of the set of values not all equal are less than their arithmetic mean. Geometric mean of n numbers is defined as the nth root of the product of n numbers. The geometric mean is used in finance to calculate average growth rates and is referred to as the compounded annual growth rate. Otherwise the geometric mean is smaller. TextGSDx etextSDlog x This is going to be useful if and only it was a good idea to use a geometric mean on your data and particularly if your data is positively skewedMake sure you realize what this is saying. Find the geometric mean for the values 3 5 6 6 7 10 12.
The geometric mean of a non-empty data set of positive numbers is always at most their arithmetic mean.
Equality is only obtained when all numbers in the data set are equal. In surveys and studies too the geometric mean becomes relevant. The geometric mean will always be smaller than the arithmetic and the harmonic will be the smallest of all. For a given set of two numbers such as 3 and 1 the geometric mean is equal to 3 1732. TextGSDx etextSDlog x This is going to be useful if and only it was a good idea to use a geometric mean on your data and particularly if your data is positively skewedMake sure you realize what this is saying. Equality is only obtained when all numbers in the data set are equal.